Version 4.0.0 had a lot of changes to the API to support better extensibility, testability, and maintainability, but the biggest change was the 30-40% improvement in performance. This type of of performance gain is huge and a boon for sure for all those using the library - but just how was it done?
If you’ve ever done performance analysis or improvements to a piece of code, you are aware that improving performance by saving one object allocation, for example, is nice, but often not very impactful. Naturally, if you’re able to find lots of those instances, these can add up, but the most impactful performance improvements come from algorithms. Choosing algorithms that are better suited to the problem, more efficient wrt. complexity, better cache locality, etc.
Specifically, this performance improvement was in the Broadphase collision detection system and how it handles detection from frame to frame.
Background
First a bit of background. dyn4j includes a system for detecting collisions between objects. This system is broken down into three main phases:
- Broadphase
- Narrowphase
- Manifold Generation
Why the 3-phase approach? The narrowphase algorithms are expensive to run, so if we can reduce the possible set of colliding pairs, then we save a lot of processing time. If we didn’t do this, we’d need to test every object with every other object. That’s \(O(n^2)\) tests - very inefficient especially when it’s more common to not be colliding than they other way around.
Thus, the broadphase is where we detect all the potential pairs of colliding objects. More specifically, it returns a set of collision pairs that may be colliding. Those pairs that are not included in this set are definitely NOT colliding. The pairs are handed over to the narrowphase where we find out if they truly are or aren’t colliding. Now, how does it do this? And how does it do it more efficiently than the narrowphase?
Broadphase Collision Detection
Broadphase collision detection algorithms center around the idea of choosing a simple bounding shape that encompasses the object. For example, let’s imagine I have a simple square shape and I want to create a bounding shape for it. I can use any type of shape I want, but clearly the choice will determine the efficiency of the algorithm. In the below picture you see three different possibilities (these are the more common choices):
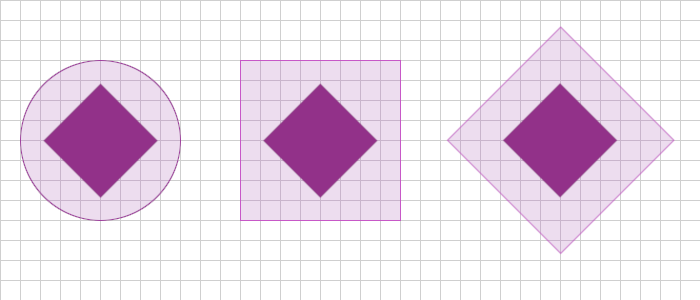
The first is a bounding circle. This bounding shape has very quick collision detection - compare the squared distance between the two objects against the sum of their radii. The downside is that long shapes create huge bounding circles. If you could guarantee that your shapes were all compact, this might be a good choice, but not for a generic collision detection system that has no idea what objects will look like.
The second is an Axis-Aligned Bounding Box, AABB for short. It’s a rectangle that’s always aligned to the x and y axes. This solves the problem that the bounding circle had where long objects would create large bounding shapes. However, what happens if that long object is rotated about it’s center - it’s the same issue as the circle bounding shape. AABB does better, but maybe not the best. To test for collision between two AABBs we only need to compare their min/max values - 4 comparisons.
The last is an Oriented Bound Box, or OBB for short. It’s a rectangle that’s always oriented with the shape. If the shape is rotated at 45 degress, then the bounding rectangle is rotated at 45 degrees. Nice! This solves our problem of rotated long objects generating huge bounding shapes. Not so fast - there’s a problem with this approach. To check for collision between two OOBs you have to use more sophisticated routines. In fact, one of those routines is effectively a narrowphase algorithm - we don’t get any benefit out of a broadphase that’s as expensive as the narrowphase.
You may have noticed that the bounding shapes in the image above didn’t exactly fit the object. This was mainly to show the differences in the bounding area, but as we’ll see soon, this is actually one of the sources of the performance enhancement being described in the post.
Having an easier collision detection proceedure isn’t all the broadphase does - we still need to contend with that \(O(n^2)\) problem. We could brute force it by testing everything against everything, but that’ll be horribly inefficient. What can we do? The answer is to subdivide the problem into smaller and smaller chunks so that when we test the higher level chunk and it’s negative, we move on - there’s no reason to do any tests against objects inside that chunk. The image below highlights this hierarchy of chunks:
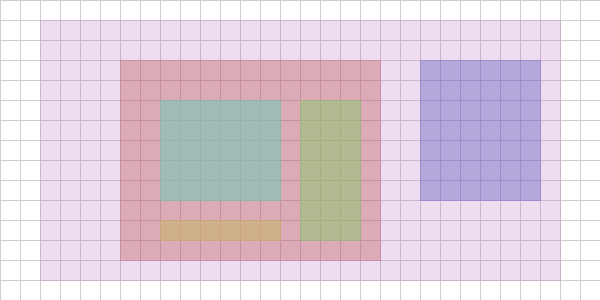
For example, if I’m testing an object’s AABB against the purple region in the image above and I detect no collision, there’s no reason to test the interior regions since they can’t possibly be colliding if the purple region isn’t. If we could build a data structure that would organize the scene in this fashion we could reduce the number of collision tests significantly. For example, if we could organize the scene into a binary tree structure, the number of tests would then be \(O(n\log_2{n})\).
There are other partitioning schemes as well: grid-based, quadtree, BSPs, etc.
Bounding shape Expansion
Creating a data structure to do less collision tests isn’t a trivial task. In addition to the creation of the initial state, we also have to keep it up-to-date as those objects move and rotate over time. It must be efficient at updating so that we don’t trade one performance issue for another. To avoid going down the rabbit hole of describing various data structures that can be used in broadphase collision detection, let’s just assume that you have one and updates to that data structure aren’t cheap.
Enter bounding shape exapansion. If you recall from the section above where we laid out a couple of options for bounding shapes, you may have noticed that the bounding shapes for the square didn’t fit around it tightly. This was primarily to highlight the different bounding shapes, but also to draw attention to the fact that they don’t have to fit tightly. Imagine I expand the bounding shape for a square and put that expanded bounding shape into the broadphase. The effect is that when the square moves/rotates, I don’t have to update the expanded bounding shape unless it leaves that expanded region.
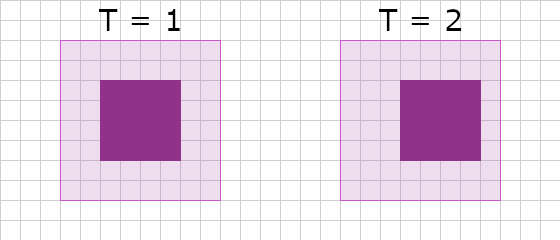
In \(T = 2\), the square only moved one unit to the right and is still fully contained in the bounding AABB. There’s no reason to update the bounding shape because it would not effect the end result.
Let’s review what we’re trying to do here - we want to send less pairs to the narrowphase, but we also want to reduce the number of updates to our data structure. Sending less pairs to the narrowphase means the expensive collision detection there is run less often. Less updates to our broadphase data structure means we do less work per frame. If we choose tighly fitting bounding shapes we get the smallest number of collision tests in the broadphase, but for every one of those objects that’s moving/rotating, the data structure will need to be updated every frame. If we choose super fat bounding shapes we end up doing more collision tests in the broadphase, but we don’t have to update the broadphase data structure as often (as described above).
The key then is to strike a balance between expanding a lot and not expanding at all. This is a configurable property in dyn4j.
The New Optimization
At this point, we have a broadphase collision detection algorithm that uses a data structure to avoid the \(O(n^2)\) number of collision tests, a collision detection test that is far quicker than the narrowphase, and we’ve chosen an appropriate bounding shape expansion to avoid rebuilding te data structure every frame. What more can be done?
To take a step back, think about how a simulation evolves over time:
- Detect collisions
- Resolve collisions
- Move objects to new positions
Or something like this:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public void runSimulation() {
while (true) {
simulationStep();
}
}
public void simulationStep() {
// get ALL broadphase collision pairs
List<Pair> pairs = broadphase.getPairs();
// filter broadphase pairs using the narrowphase
Iterator<Pair> iterator = pairs.iterator();
while (iterator.hasNext()) {
Pair pair = iterator.next();
if (!narrowphase.detect(pair)) {
// then remove it
iterator.remove();
}
}
// resolve collisions
// ...
// move objects to new positions
// ...
}
This flow would be called for every frame of the simulation. Thus, for every frame we have to retest everything with everything. this seems like a lot of work, but it makes sense - we need to make sure that new collisions are detected and old collisions are no longer handled. The magic for the improved performance in dyn4j 4.0.x lies in this process.
Imagine that we have the following configuration on frame 1 of our simulation:
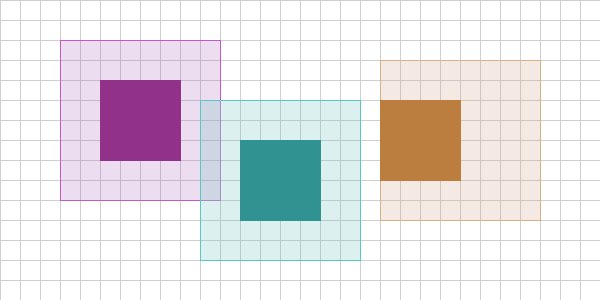
We have three squares with expanded bounding shapes (AABBs in this case). The purple and teal expanded bounding shapes are overlapping. The orange object’s expanded bounding shape is offset because the orange object moved last frame. Also imagine the purple object is moving as well, but the teal object is stationary. In this setup we have 3 objects and therefore 3 collision tests to do in the worst case (brute-force). Purple vs. Teal, Purple vs. Orange, Teal vs. Orange.
We don’t test Purple vs. Teal and Teal vs. Purple as this would give the same result.
Next, imagine the simulation proceeds to frame 2:
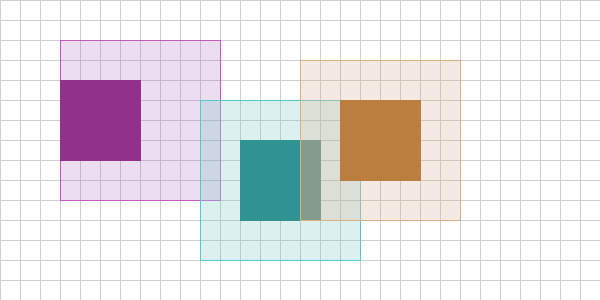
The purple and orange object have moved two units to the left while the teal object stayed stationary. Notice that the purple object’s expanded bounding shape remained the same, but the orange object’s expanded bounding shape changed. Now, think critically here - from the last frame to this frame, what do we really need to test? Everything again?
You’ve probably already guessed it, but no we don’t. The collision between the purple and teal objects hasn’t changed - no reason to test it again. That said, the orange object’s expanded bounding shape did change, so we have to test that. That means in frame 2 we only do 2 collision tests! Orange vs. Teal and Orange vs. Purple. Therefore, the performance enhancement we can make is to track, over time, the collisions between objects in the broadphase and only re-test those that have had their expanded bounding shapes updated.
KEY: Therefore, the performance enhancement we can make is to track, over time, the collisions between objects in the broadphase and only re-test those that have had their expanded bounding shapes updated.
Enhancing our code from before:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// ...
List<Pair> pairs = new ArrayList<Pair>();
public void simulationStep() {
// get only the NEW broadphase collision pairs
List<Pair> bpairs = broadphase.getNewPairs();
// filter broadphase pairs using the narrowphase
for (Pair pair : bpairs) {
if (narrowphase.detect(pair)) {
// then track it in our cross frame set of pairs
pairs.add(pair);
}
}
// ...
}
Ok, great - this is cool and all, but how do we handle frame 3 of the simulation:
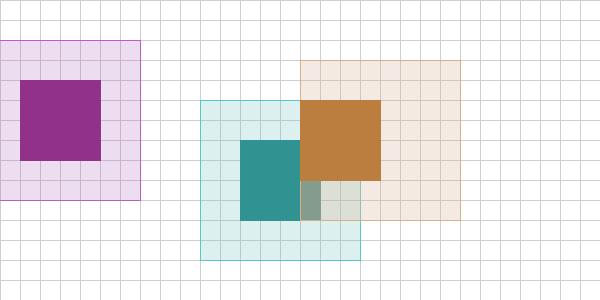
In this frame, we see that the teal and orange object’s bounding shapes have not moved, but the purple object’s has. As a result, we only test Purple vs. Teal and Purple vs. Orange and find neither is colliding. If the contract for our broadphase is to only return potentially colliding pairs, it would return nothing. But how would we know that the collision between Purple and Teal is no longer happening?
It turns out the answer is pretty simple, as you go through ALL the stored pairs, remove those who’s bounding shapes are no longer colliding:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
// ...
List<Pair> pairs = new ArrayList<Pair>();
public void simulationStep() {
// get only the NEW broadphase collision pairs
List<Pair> bpairs = broadphase.getNewPairs();
// add them to the set of pairs from the last frame
// obviously you'll need to make sure you don't add
// a pair that already exists in the pair list from
// last frame - I'm not doing that here for simplicity
for (Pair pair : bpairs) {
pairs.add(pair);
}
// filter out those that are no longer colliding
Iterator<Pair> allIterator = pairs.iterator();
while (allIterator.hasNext()) {
Pair pair = allIterator.next();
if (!pair.isBoundingShapeOverlapping()) {
// then remove it
allIterator.remove();
continue;
}
// filter broadphase pairs using the narrowphase
if (narrowphase.detect(pair)) {
// then continue processing the collision...
}
}
}
You might say at this point, “wait a minute, we’re doing collision tests with the expanded bounding shapes again - isn’t that even worse?” It turns out no, the key being that we’re not doing it for ALL pairs, only those that are currently tracked as potentially overlapping. We’ve changed the algorithm from \(O(n\log_2{n})\), for example, to \(O(m\log_2{n})\), where \(m\) is the number of objects who’s expanded AABBs have been updated.
Evaluation
Let’s evaluate the improvement with some numbers and assumptions. Assume we have a scene with 5000 objects. Of those 5000 objects, 500 are moving every frame. Of those 500 moving objects, 50 of them need to update their expanded shapes every frame. Assume that of all 5000 objects we have 1000 collisions. Finally, assume that our broadphase has complexity \(n\log_2{n}\) to do all tests.
| Scenario | Formula | Tests | % |
|---|---|---|---|
| No enhancement with or without bounding shape expansion. | \(5000\log_2{5000}\) | 61,438 | - |
| With enhancement but without bounding shape expansion. | \(500\log_2{5000} + 1000\) | 7,143 | 87% |
| With enhancement and bounding shape expansion. | \(50\log_2{5000} + 1000\) | 1,614 | 97% |
The \(+ 1000\) in the above forumlas account for re-testing of overlap to account for objects moving out of collision (as described in the Frame 3 discussion in previous section).
From scenario 1 to 3 that’s nearly a 100% decrease in the number of tests - wow! Clearly, the numbers I chose were to highlight the improvement, but the gains will be highly dependent on your simulation. You could think of scenario 2 being the worst case for this enhancement and scenario 3 being the best case. These numbers are also dependent on the value used to expand the bounding shapes and the ratio of static vs. moving shapes in your scene. If all 5000 objects were moving and we chose an expansion value that forced an update for all objects every frame, then we’re worse off than where we started. Also keep in mind that the storage and maintenance of the frame to frame collision data has overhead.
dyn4j saw anywhere between 30-40% raw performance increase implementing this simple enhancement (measuring the same simulations before/after the enhancement)
A positive side effect of tracking the collisions from frame to frame is that we can reduce allocation by storing the results and reusing those objects for the next frame. In addition, we can build new API surface that enables callers to query this information outside of the standard listener pattern giving them more opportunity to do things in a simpler manner.
