The last installment talked about the GJK algorithm as it pertains to collision detection. The original algorithm actually is used to obtain the distance and closest points between two convex shapes.
Introduction
The algorithm uses much of the same concepts to determine the distance between the shapes. The algorithm is iterative, uses the Minkowski Sum/Difference, looks for the origin, and uses the same support function.
Overview
We know that if the shapes are not colliding that the Minkowski Difference will not contain the origin. Therefore instead of iteratively trying to enclose the origin with the simplex, we will want to generate a simplex that is closest to the origin. The closest simplex will always be on the edge of the Minkowski Difference. The closest simplex for 2D could be either a single point or a line.
Minkowski Sum
Just as we did for the collision detection portion of GJK in the previous post, the algorithm also needs to know the Minkowski Sum (Difference is what I will call it, see the GJK post).
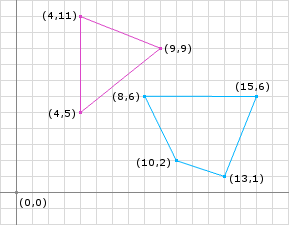
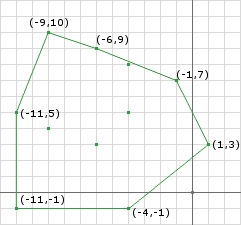
Taking the same shapes from the GJK post and separating them (Figure 1) yeilds the same Minkowski Difference only translated slightly (Figure 2). We notice that the origin is not contained within the Minkowski Difference, therefore there is not a collision.
The Distance
The distance can be calculated by finding the closest point on the Minkowski Difference to the origin. The distance is then the magnitude of the closest point. By inspection, we see that the edge created by the points (-4, -1) and (1, 3) is the closest feature to the origin. Naturally the closest point to the origin is the point on this edge that forms a right angle to the origin. We can calculate the point by:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A = (-4, -1)
B = (1, 3)
// create the line
AB = (1, 3) - (-4, -1) = (5, 4)
AO = (0, 0) - (-4, -1) = (4, 1)
// project AO onto AB
AO.dot(AB) = 4 * 5 + 1 * 4 = 24
// get the length squared
AB.dot(AB) = 5 * 5 + 4 * 4 = 41
// calculate the distance along AB
t = 24 / 41
// calculate the point
AB.mult(t).add(A) = (120 / 41, 96 / 41) + (-4, -1)
= (-44 / 41, 55 / 41)
= (-1.07, 1.34)
d = (-1.07, 1.34).magnitude() = 1.71
This is a simple calculation since we know what points of the Minkowski Difference to use.
Iteration
Like the collision detection routine of GJK the distance routine is iterative (and almost identical for that matter). We need to iteratively build a simplex which contains the closest points on the Minkowski Difference to the origin. The points will be obtained using a similar method of choosing a direction, using the support function, and checking for the termination case.
Lets examine some psuedo code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
// exactly like the previous post, use whatever
// initial direction you want, some are more optimal
d = // choose a direction
// obtain the first Minkowski Difference point using
// the direction and the support function
Simplex.add(support(A, B, d));
// like the previous post just negate the
// the prevous direction to get the next point
Simplex.add(support(A, B, -d));
// obtain the point on the current simplex closest
// to the origin (see above example)
// start the loop
d = ClosestPointToOrigin(Simplex.a, Simplex.b);
while (true) {
// the direction we get from the closest point is pointing
// from the origin to the closest point, we need to reverse
// it so that it points towards the origin
d.negate();
// check if d is the zero vector
if (d.isZero()) {
// then the origin is on the Minkowski Difference
// I consider this touching/collision
return false;
}
// obtain a new Minkowski Difference point along
// the new direction
c = support(A, B, d);
// is the point we obtained making progress
// towards the goal (to get the closest points
// to the origin)
double dc = c.dot(d);
// you can use a or b here it doesn't matter
// since they will be equally distant from
// the origin
double da = Simplex.a.dot(d);
// tolerance is how accurate you want to be
if (dc - da < tolerance) {
// if we haven't made enough progress,
// given some tolerance, to the origin,
// then we can assume that we are done
// NOTE: to get the correct distance we
// need to normalize d then dot it with
// a or c
// OR since we know that d is the closest
// point to the origin, we can just get
// its magnitude
distance = d.magnitude();
return true;
}
// if we are still getting closer then only keep
// the points in the simplex that are closest to
// the origin (we already know that c is closer
// than both a and b so we only need to choose
// between these two)
p1 = ClosestPointToOrigin(Simplex.a, c);
p2 = ClosestPointToOrigin(c, Simplex.b);
// getting the closest point on the edges AC and
// CB allows us to compare the distance between
// the origin and edge and choose the closer one
if (p1.magnitude() < p2.magnitude()) {
Simplex.b = c;
d = p1;
} else {
Simplex.a = c;
d = p2;
}
}
The first few lines look a lot like the previous GJK post. The difference is the building of our simplex. We are using the same idea of a simplex, we use the same support function and roughly the same logic, however, we only keep 2 points at all times (3D would be 3 points) and we find a point on the simplex closest to the origin instead of finding the Voronoi region that the origin lies in.
As we did in the previous post this is best explained by running through an example. Let’s take the example above from Figure 1 and run through the iterations.
Pre Iteration:
1
2
3
4
5
6
7
8
9
// im going to choose the vector joining the
// centers of the objects as the initial d
d = (11.5, 4.0) - (5.5, 8.5) = (6, -4.5)
Simplex.add(support(A, B, d)) = (9, 9) - (8, 6) = (1, 3)
Simplex.add(support(A, B, -d)) = (4, 11) - (13, 1) = (-9, 10)
// calculate new d (for brevity, we'll just look at figure 4)
d = (1, 3) // then negate
d = (-1, -3)
// start the iterations</pre>
Iteration 1:
1
2
3
4
5
6
7
8
9
10
11
// get a new point in this direction
c = support(A, B, d) = (4, 5) - (15, 6) = (-11, -1)
// are we still moving closer to the origin?
dc = 11 + 3 = 14
da = -1 - 9 = -10
// 14 - -10 = 24 not small enough
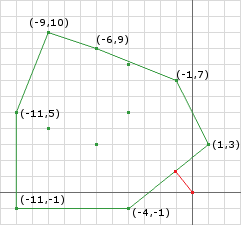
// by inspection, edge AC [(1, 3) to (-11, -1)] is closer than BC [(-9, 10) to (-11, -1)]
// so keep a and replace b with c
b = c
// use p1 as the next direction
d = p1
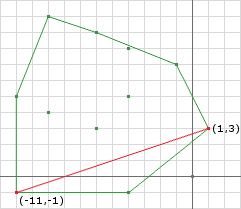
In this first iteration I didn’t go through the trouble of calculating p because its obviously going to be the end point a. If you performed the real calculation, like the code will do, you will obtain the same result. We notice that even though the closest point is a point already on the simplex, we can still use it as the next direction. We obtain a new point using the new direction and keep the two closest points.
Iteration 2:
1
2
3
4
5
6
7
8
9
10
11
12
d = (0.8, -2.4)
// get a new point in this direction
c = support(A, B, d) = (4, 5) - (8, 6) = (-4, -1)
// are we still moving closer to the origin?
dc = -3.2 + 2.4 = -0.8
da = 0.8 - 7.2 = -6.4
// -0.8 - -6.4 = 5.6 not small enough
// by inspection, edge AC [(1, 3) to (-4, -1)] is closer than BC [(-11, -1) to (-4, -1)]
// so keep a and replace b with c
b = c
// use p1 as the next direction
d = p1
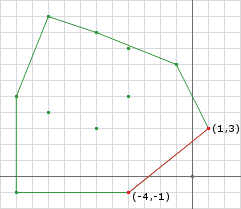
Notice that our simplex is getting closer to the origin.
Iteration 3:
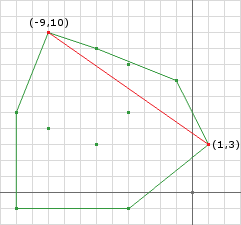
Notice in iteration 3 that d is the closest point to the origin and is the same point we found in the Distance section above.
1
2
3
4
5
6
7
8
9
10
d = (1.07, -1.34)
// get a new point in this direction
c = support(A, B, d) = (9, 9) - (8, 6) = (1, 3)
// are we still moving closer to the origin?
dc = -1.07 + 4.02 = 2.95
da = -1.07 + 4.02 = 2.95
// 2.95 - 2.95 = 0 i think thats small enough!
// ||d|| = 1.7147886...
// we done!
distance = 1.71
We notice that when we terminated the difference in projections was zero. This can only happen with two polygons. If either A or B was a shape with a curved edge the difference in projections would approach zero but not obtain zero. Therefore we use a tolerance to handle curved shapes since the tolerance will also work for polygons.
Another problem curved shapes introduce is that if the chosen tolerance is not large enough the algorithm will never terminate. In this case we add a maximum iterations termination case.
One more problem that this algorithm can run into is if the shapes are actually intersecting. If they are intersecting the algorithm will never terminiate. This isn’t as big of a problem since most of the time you will determine if the shapes are colliding first anyway. If not, then we must add a check in the while loop for the simplex containing the origin. This can be done by a simple point in triangle test (2D).
Closest Points
In addition to the distance between the two shapes, we can also determine the closest points on the shapes. To do this we need to store additional information as we progress through the algorithm. If we store the points on the shapes that were used to create the Minkowski Difference points we can use them later to determine the closest points.
For instance, we terminated above with the Minkowski Difference points A = (1, 3) and B = (-4, -1). These points were created by the following points on their respective shapes:
Shape Points
| S1 | S2 | Minkowski Point | |
|---|---|---|---|
| a | (9, 9) | (8,6) | = (1, 3) |
| b | (4, 5) | (8,6) | = (-4, -1) |
The points used to create the Minkowski Difference points are not necessarily the closest points. However, using these source points we can calculate the closest points.
Convex Composition
We see that the points from A and B are not the correct closests points. By inspection we can see that the closest point on B is (8, 6) and the closest point on A is roughly (6.75, 7.25). We must do some calculation to obtain the closest points. Here’ where the definition of a Convex Combination comes in:
\[\begin{align} CC(S) &= \sum_{i=1..n} \lambda_i\vec{p}_i = \lambda_1\vec{p}_1 + ... + \lambda_n\vec{p}_n \:\textrm{where}\: \vec{p}_i \in S \:\textrm{and}\: \lambda_i \in \mathbb{R} \\ \sum_{i=1..n} \lambda_i &= 1 \:\textrm{where}\: \lambda_i >= 0 \end{align}\]We can guarantee that the points we attempt to find will be on the simplex since all convex combinations are within the convex hull of the set \(S\). Any positive values for the \(\lambda\) coefficients ensure we don’t overstep the bounds of the simplex. Our 2D example looks like this:
\[CC(S) = \lambda_1\vec{p}_1 + \lambda_2\vec{p}_2\]Next, let’s say that \(\vec{q}\) is the closest point to the origin on the termination simplex, then we know that the vector from \(\vec{q}\) to the origin must be perpendicular to the line segment \(\vec{l}\) that \(\vec{q}\) lies on. We also know that \(\vec{q}\), because it lies on the edge of the simplex it can be defined as a convex combination of the points \(\vec{a}, \vec{b}\) that make up the line segment \(\vec{l}\).
\[\begin{align} \vec{q} \cdot \vec{l} &= 0 \\ (\lambda_1\vec{a} + \lambda_2\vec{b}) \cdot \vec{l} &= 0 \end{align}\]We need to solve for \(\lambda_1\) and \(\lambda_2\), but to do so we need 2 equations. The second equation comes from the other part of the definition of a convex combination:
\[\begin{align} \sum_{i=1..n} \lambda_i &= 1 \:\textrm{where}\: \lambda_i >= 0 \\ \lambda_1 + \lambda_2 &= 1 \end{align}\]Solving the system of equations we obtain:
\[\begin{align} \lambda_1 + \lambda_2 &= 1 \\ \lambda_1 &= 1 - \lambda_2 \\ \\ (\lambda_1\vec{a} + \lambda_2\vec{b}) \cdot \vec{l} &= 0 \\ ((1 - \lambda_2)\vec{a} + \lambda_2\vec{b}) \cdot \vec{l} &= 0 \\ (\vec{a} - \lambda_2\vec{a} + \lambda_2\vec{b}) \cdot \vec{l} &= 0 \\ (\vec{a} + \lambda_2(\vec{b} - \vec{a})) \cdot \vec{l} &= 0 \\ \vec{a} \cdot \vec{l} + \lambda_2\vec{l} \cdot \vec{l} &= 0 \\ \lambda_2\vec{l} \cdot \vec{l} &= -\vec{a} \cdot \vec{l} \\ \lambda_2 &= -\frac{\vec{a} \cdot \vec{l}}{\vec{l} \cdot \vec{l}} \end{align}\]If we perform this computation on our example above, we get:
1
2
3
4
5
l = (-4, -1) - (1, 3) = (-5, -4)
ldotl = 25 + 16 = 41
ldota = -5 - 12 = -17
lambda2 = 17/41
lambda1 = 24/41
After computing \(\lambda_2\) and \(\lambda_1\) we can compute the closest points by using the definition of the convex combination again, but using the points that made up the Minkowski Difference points (remember that s1 and s2 of A and B were listed in the table above):
1
2
3
4
aClosest = lambda1 * As1 + lambda2 * Bs1
bClosest = lambda1 * As2 + lambda2 * Bs2
aClosest = 24/41 * (9, 9) + 17/41 * (4, 5) = (6.93, 7.34)
bClosest = 24/41 * (8, 6) + 17/41 * (8, 6) = (8, 6)
As we can see we computed the closest points!
There are a couple of problems here we must resolve however.
First, if the Minkowski Difference points \(\vec{a}\) and \(\vec{b}\) are the same point, then \(\vec{l}\) will be the zero vector. This means that later when we divide by the magnitude of \(\vec{l}\) we’ll divide by zero: not good. What this means is that the closest point to the origin is not on a edge of the Minkowski Difference but is a point. Because of this, the support points that made both \(\vec{a}\) and \(\vec{b}\) are the same, and therefore you can just return the support points of \(\vec{a}\) or \(\vec{b}\):
1
2
3
4
if (l.isZero()) {
aClosest = a.s1;
bClosest = a.s2;
}
The second problem comes in when either \(\lambda_1\) or \(\lambda_2\) is negative. According to the definition of a convex hull, \(\lambda\) must be greater than zero. If \(\lambda\) is negative, this tells us that the support points of the other Minkowski Difference point are the closest points:
1
2
3
4
5
6
7
if (lambda1 < 0) {
aClosest = b.s1;
bClosest = b.s2;
} else if (lambda2 < 0) {
aClosest = a.s1;
bClosest = a.s2;
}
Comments
62 responses
Rodrigo,
Sorry for the late response. Now I just to remember how this works....
To answer the first question: You are right that (1.7, 2.51) is the closest point if the simplex was a line, since it isn't, the closest point is the end point of the line segment. Now I haven't fully thought it through yet, but it may not matter because you still obtain a vector in that points to the same Voronoi region of the simplex. Ideally, I think you would want d to always be the simplex normal in the direction of the origin.
The second question is bit tricky: What you have found here is a degenerate case! If you look closely, the origin actually lies on the line created by the simplex points, thereby causing the result to be zero. Even if you do something like what I suggested in the first questions answer, this can still happen depending on the method you arrive at the closest point. So in this case, you do have to do something different, which is keep the points who are closest to the origin (so you must pick 2 of the 3). What you have suggested is similar to what I do as well.
In iteration 3, after finding the new direction d(0.62, -0.78), then the point in that direction should be (-4,-1). It is the same with the point added in the iteration 2. My reason is (-4,-1) dot (0.62,-0.78)=-1.7. It is larger than the dot product of (1,3) and (0.62,-0.78)=-1.72. Would you please tell me why you choose (1,3) here? Thanks very much.
The other point could have been chosen as well. If we use better precision than in the examples above the choice to use the point (9, 9) or (4, 5) becomes apparent:
d.dot(4, 5) = -1.405563856997454589716925831015
d.dot(9, 9) = -1.405563856997454589716925831017
You'll notice that (9, 9) is insignificantly smaller than (4, 5) and if in your code you use floating point variables, they will be identical. This is the case because the direction vector is the normal of the edge (9, 9) to (4, 5) and therefore the projection of both points should be the same.
In these cases, you can use either one, it doesn't matter, you'll get the same result!
I notice that in this post, you first find the new point P = AB.mult(t).add(A), then the search in the direction of -P. While in the previous post, the direction is found by doing the triple cross product. What's the reason for this? Thanks.
I'm trying to use this case to see how to jump out of the loop. Starting with A(1,3) and B(-9,10), then doing triple cross product ABxAOxAB give the direction (-0.573,-0.819). Then I use all the vertices on the edge to dot product with the direction vector. For 3 vertices give positive values and vertex (-11,-1) gives the largest one (Question 1: Here, should I check if the simplex contains the origin?).
So (-11,-1) is added on as the new point A, same as in your post. Then I do the triple cross product to find the direction (0.316, -0.949) to search. doing dot product of all vertices with the new searching direction gives all negative values. So, question 2, does it mean the loop should be terminated here? or should I keep on searching in another direction until it leads back to the vertex that has already been checked before? Cuz when I keep on doing triple cross product to find the new point, it leads me to (-4,-1), and then back to (1,3) where I started.
Thanks a lot for answering all my questions.
That's a good observation. The reason they are done differently is because of the assumptions. In the first post we are making the assumption that the origin lies within the Minkowski sum, terminating when we verify this (or cannot verify). Because we need to know where the origin lies (by voronoi regions) and find a new search direction, we just put the two together.
Finding the distance is similar but slightly different. No longer are we checking if the simplex contains the origin since the assumption is that the Minkowski sum does not contain the origin. In addition, the simplex is a line segment, instead of a triangle, and therefore cannot contain the origin (if we ignore cases where the origin is on the line segment). Because of this we don't need to worry about voronoi regions or where the origin lies. The search direction is always the normal of the line segment in the direction of the origin.
Given that, I chose to use P = AB.mult(t).add(A) which obtains the point on the line segment that is closest to the origin so that when the loop terminates I'll be able to get the separation distance by simply getting the magnitude of P.
No problem, these questions will help everyone who reads them.
As for question 1: You do not have to check if the simplex contains the origin. The simplex in the distance check is a line segment anyway and can only "contain" the origin if the origin lies on the line segment, in which case you must determine if this is considered a collision or not. You may have noticed that in my code I do check if the origin lies within the triangle (before throwing away one of the points). I do this because my distance method can be called by anyone, and they may not know that the distance method assumes that the shapes are separated. Otherwise I would remove that check.
As for question 2: Right, the termination case is a bit tricky. The termination condition in this algorithm is when the projection of the simplex points are equal (a better one, which is what I use in the post, is to test if the difference in the projection of the simplex points is below some tolerance).
So in iteration 1, you find c, the new point, to be (-11, -1). If we project this onto the search direction along with either of the current simplex points and subtract these we get 7.64, which is not small enough to end.
So in iteration 2, you find c to be (-4, -1). If we do the same thing here we get 2.2, which again is not small enough to end.
Now in iteration 3, you find c to be (1, 3). If we do the same thing again we get 0, which is less than our tolerance, so we end the loop.
What this means is that the simplex (the red line segment) cannot get any closer to the origin.
So right now my understanding is:
If we have two objects in interaction, then we'll always be able to locate at least one point giving a positive dot product in the direction we're searching for. And for each point added in, we can generate a simplex to determine if it contains the origin. And eventually we'll find such origin.
If the two objects are not in contact, we'll soon jump out of the loop when we can not find any points giving positive "dot product".
Is it correct?
One more question, I'm trying to do a 3D case. So I need to build a triangle first then add a point in the search direction to get a tetrahedron. How to get the first triangle? With the same method in 2D, I can easily find a line segment, then doing a triple cross product will give a third point and thus generating a triangle. Do you think this can be the triangle to start with? thanks.
Yes, you are correct.
For the 3D case you can build a triangle (after building the line segment) by obtaining a normal of the line segment in the direction of the origin:
d = // choose some direction // get the first point Simplex.add(support(A, B, d); // get the second point Simplex.add(support(A, B -d); // now we have a line segment // perform the triple product to obtain a new search direction a = Simplex[0]; b = Simplex[1]; ab = b - a; ao = -a; // same thing as ORIGIN - a d = tripleProduct(ab, ao, ab); // be careful here because if the origin lies on the line ab then this will yield the zero vector // now get the last point to make the triangle Simplex.add(support(A, B, d); // now you can start the loop
Now that you have a triangle your next search direction would be the surface normal of the triangle in the direction of the origin. Then obtain a support point, then reduce the 4 points to 3.
Hi William,
First of all, thanks for the great articles you've put online!
I've been playing with an implementation in C#/WPF based on this text and the dyn4j code. Everything looks quite alright but there is an small issue with the closest point that you might be able to give me some hints on.
I have the following (default) quadrant setup;
4 | 1
——–
3 | 2
the origin (0,0) is in the middle of my screen. q1 = x > 0 && y > 0; q2 = x > 0 && y < 0 and so on.
The results look fine whenever I keep both polygons inside the first quadrant. i.e. all the vertices have a positive value. As soon as I move one or more shapes to a different region the closest points start to drift. Is this something you've seen before using this algorithm or am I overlooking a minus sign somewhere and just need to look harder?
Thanks!
Ernst
b.t.w. I'm in 2d as you might have guessed.
No I haven't seen that behavior before. What do you mean by drift?
The first thing I would check is if the distance check is working correctly minus the closest points in all quadrants. Then I would make sure that the Minkowski points are correct. The Minkowski points should be the points on the Minkowski sum that form the edge that is closest to the origin (see Figure 6).
If you still can't find the problem you are welcome to send me the code via email or by posting it here.
William
Thanks for your reply! By drifting I mean that the points leave the polygon and lag behind if you move the polygon around. It's perhaps a bit difficult to explain in text but it looks as if the closest points have a smaller radius of action.
That's a good suggestion and thanks for your offer. I'll check if the points fall onto the sum shape. Maybe there is an error I can spot.
I'll let you know!
thanks,
Ernst
right.... it looks like this was a drawing error and not an algorithmic one!
I was using the Margin property of an Ellipse to define it's offset from the borders.
This works as long as positive integral values are provided. Negative, non-integral values for margin values are technically permitted, but should be avoided because they are rounded by the layout rounding behavior.
This perfectly explains the behavior I was seeing where points would ‘lag behind' a shape.
Again, thanks for you suggestions. It helped me verify the points where chosen correctly but just drawn incorrectly.
On to the EPA article :)
cheers!
Ernst
Dear William:
I'm not so clear what the following is used for.
c = support(A, B, d) = (4, 5) – (15, 6) = (-11, -1)
// is c far enough along d
dc = 3.52 + 0.95 = 4.47
da = -0.32 – 2.85 = -3.17
// 4.47 – -3.17 = 7.64 not small enough
What does it mean the c is far enough along d ?
Thx a lot!
@Futurecoming
Yeah, I can see how that is a little confusing. Its a carry over comment from the GJK collision detection post. I updated this post to better explain whats happening.
To explain a little further:
We are basically checking to make sure we are making progress. Progress, in this case, is defined by getting closer to the origin. In other words, we are checking to make sure that the points we store in the simplex are the closest ones that we have found so far. This will ensure, after a few iterations, that we will get the closest simplex to the origin, and from there, the closest points.
William
Hey, I recently implemented SAT for 3d collision detection. I'm just wondering what the benefits are of SAT and GJK. Thanks!
@John
I'll try to summarize the major benefits of each, but this is by no means a complete list. The tough part is that both are really good algorithms and really only have small benefits over one another.
SAT Pros:
1. Very easy to implement and debug.
2. Returns collision normal and depth when a collision is detected.
3. Can be implemented on the GPU really easily (and will be extremely fast).
4. Really fast.
SAT Cons:
1. Really only designed to work with polygons/polyhedra. You can make it work for circular curves or just use polygonal approximations of curves.
2. In 3D you may end up tests a lot of axes in the collision case, especially if you end up approximating curved shapes (not really an issue for the GPU).
3.
GJK Pros:
1. Very elegant implementation, for OOP especially.
2. With very minor code changes it can be used to return the distance between two convexes and their closest points.
3. Can handle any kind of convex shape, all that's required is a support function for it.
4. Really fast, even in the collision cases.
GJK Cons:
1. Slightly harder to understand, implement and debug.
2. Harder to get numerically stable.
3. Requires a separate algorithm to return collision normal and depth when a collision is detected (EPA, sampling, etc.)
4. Not as easily transferable to the GPU due to the number of branches in the code.
If you've already implemented one of these, I would just stick with it until the need arises where you need the other for some reason.
William
Hi,
I implemented the GJK algorithm for 3D case. The code runs fine but I am not able to get a grasp on the terminating condition.
I quote your comment "Right, the termination case is a bit tricky. You know to terminate the loop when the new point you found via the support function is projected onto the search direction and that projection is not greater than zero. "
But in iteration 2, your dc value is -0.33 and in the next iteration it is -1.72. So shouldn't it have ended at iteration 2 itself? when the value of dc became negative.
Also, the termination condition is checking for dc-da. Can you explain that further?
Also, I am using the same terminating condition for 3D case and so far there are no problems. Is the terminating condition which you have stated here valid for 3D case as well?
@Vishal
I think that I was answering too many questions in that response, so its a bit confusing. I have updated it to make more sense.
What we are doing is testing the projections of the current simplex points and the new simplex point we just found. So dc represents the projection of the new simplex point onto the support direction. da represents the projection of one of the current simplex points onto the support direction (it doesn't matter which). These projections tell us how far away from the origin they are. Doing dc – da tells us if we are getting closer or farther away from the origin as we are iterating. Eventually, the projections, dc and da, will be near equal which indicates that we've found the closest edge (feature in your case) to the origin.
William
Thanks! Now it is clear to me. I drew a few diagrams to understand what you meant and now I understand completely.
i think convex hull is a set of point and no more.
i don't really what is lambda :-?
CH(S) = ∑i=1…n λiPi = λ1P1 + … + λnPn
@karim
I've updated these sections to better reflect the concept being used: a Convex Combination.
To explain a little further: we obtained the final simplex [A,B], which is a line segment in 2D, at the termination of the algorithm. The line segment can be considered a convex hull. We can find any point inside or on the edge of the hull by using a convex combination of any of the points within the hull (in our case we use all the vertices which make up the convex hull). Since the simplex is within the Minkwoski Difference, which is a linear combination of two convex shapes, the lambda scalars can be used in the same manner on the individual shape's closest edges [A1,B1] and [A2,B2] to find the closest points.
William
Thank you very much.
i think i got. but another question, how we achieve this equation:
λ2 = -L · A / (L · L)
?
sorry if i bother you.
@karim
Nope, it's no trouble.
We have two equations with two unknowns: λ1 and λ2. Our equations are:
(λ1A + λ2B) · L = 0 λ1 + λ2 = 1
Solve one of the equations for λ1. (I'll solve the 1st equation)
// Distribute the dot product of L λ1A · L + λ2B · L = 0 // We can factor out the lambdas since they are scalars λ1(A · L) + λ2(B · L) = 0 // Move the λ2(B · L) term to the other side λ1(A · L) = -λ2(B · L) // Divide by (A · L) λ1 = (-λ2(B · L)) / (A · L)
Then substitute this into the other equation.
(-λ2(B · L)) / (A · L) + λ2 = 1
Then solve for λ2
(-λ2(B · L)) / (A · L) + λ2 = 1 // Multiply everything by (A · L) -λ2(B · L) + λ2(A · L) = (A · L) // Factor out λ2 since its a scalar λ2(A · L - B · L) = (A · L) // Factor out the dot product with L (since its distributive) λ2((A - B) · L) = (A · L) // Remember that L = B - A -λ2(L · L) = (A · L) // Divide by L · L λ2 = -(A · L) / (L · L)
To find λ1, substitute λ2 into the λ1 + λ2 = 1 equation.
William
Hi William,
Thanks for a great post!
I want to find the distance between two cubes (3D). The cubes are oriented bounding boxes. Can I follow the same procedure as you are doing in this post to find the minimum distance? My first thought is that I will also need to include the cube faces somehow. It is not enough to only check distance against line segments. I look over all replies and found the one you wrote to Ray Zong 8.feb 2011 but I am not sure if he is talking about checking for origo inside the rectangles and not finding the distance.
Appreciate all help you can provide. Thanks again!
BR
aadne
@aadne
Yes, Ray Zong is asking the same question. In 3D you'll need to keep a triangle rather than a line segment as the simplex. From there, the algorithm is mostly the same:
1. Get the normal of the simplex in the direction of the origin. NOTE: A triangle has two normals in 3D, you want the one that points towards the origin.
2. Get a support point in the direction of the origin.
3. Check if the point from #2 is farther along the direction from #1 as compared with any point of the simplex.
a. If yes, then remove a point from the simplex, add the point from #2 to the simplex, and go back to #1. NOTE: you want to keep the two points from the simplex that are closest to the origin. If there's a tie, you'd want to keep the points whose area is the largest.
b. If no, then we have a triangle on the closest face to the origin.
From here you just need to find the distance from the face to the origin. This could get tricky since you need the distance to the closest point on the Minkowski Sum's face which may not be the same as the distance to the closest point on the simplex.
William
@William
Ok. Thanks for your reply. So I guess I can use a "Distance between a plane (closest face) and a point (origin)" calculation. I guess I also should include calculation of the distance from the closest point(vertex) and maybe line segment(edge) to origin. This will cover distances from the vertices and edges of my cube. Then when I have all three distances (face, point (vertex) and line segment, edge) to origin, I can pick the one with the shortest distance. This will be the minimum distance between the two cubes.
So to conclude GJK – Distance algo seems to be a solution to find the closest face between two cubes and from here I will have the closest point (vertex) and edge.
Hi William.
How can I figure out if the normal of my triangel face is pointing towards origin? Ref step 1 in your answer to me 31 July.
Br aadne
@aadnevik
You can get the normal of triangle in the direction of the origin by first getting either normal of the triangle. Then project the vector from any point on the triangle to the origin onto the normal. If the projection is negative, then negate the normal.
simplex = // has 3 vertices since its a triangle
v1 = simplex[2] - simplex[1]; // vertex 1 to vertex 2
v2 = simplex[0] - simplex[1]; // vertex 1 to vertex 0
normal = v1.cross(v2);
// project the origin and any of the simplex vertices
// onto the normal. If the origin is behind the plane
// then just negate all the components
vo = origin - simplex[1];
if (normal.dot(vo) < 0) {
normal.negate();
}
William
Hello again William,
I would like to find the point (on the closest face of Minkowski Sum) closest to origin. The problem is that the point found might not be inside the face. It will be on the plane, but outside its face. So I will need a check whether the point found is inside or outside. This should be easy to figure out if I only knew the fourth (4) minkowski sum point on this face. (I get a triangle on closest face from GJK). Since I am dealing with OBBs (find minimum distance between 2 OBBs in 3D) my minkowski sum shape will also be an OBB. So how can I find this last point for the current closest face? I get a triangle from GJK (3 points in minkowski sum) but I actually need all 4 points in order to know if the closest point found is actually inside the rectagle based face. I hope you understand my question and could give some help. Thanks!
@aadne
You should be able to get the closest point within the triangle, which is a start, but not necessarily the closest for the face. I haven't went much further than this.
Thinking out loud, I wonder if you could do something similar to EPA, where you expand out the simplex on that face? I'm not sure what the details would be but it might be one option.
William
Hi, William
Thanks for the great tutorial.
I also read the code in GJK.java of dyn4, which confuses me in one of the terminating conditions in the distance method.
// get the distance to the origin
double p1Mag = p1.getMagnitudeSquared();
double p2Mag = p2.getMagnitudeSquared();
// check if the origin lies close enough to either edge
if (p1Mag <= Epsilon.E) {
// if so then we have a separation (although its
// nearly zero separation)
d.normalize();
separation.distance = p1.normalize();
separation.normal = d;
this.findClosestPoints(a, c, separation);
return true;
} else if (p2Mag <= Epsilon.E) {
// if so then we have a separation (although its
// nearly zero separation)
d.normalize();
separation.distance = p2.normalize();
separation.normal = d;
this.findClosestPoints(c, b, separation);
return true;
}
Why it is a separation when the origin is very close to either edge? Is there an assumption that an overlap detection run before the distance method? And I also don't know why the normal of the separation is like that in this case, I think neither d nor p1(p2) is appropriate here.
Looking forward to your reply, Thanks!
@Yize
If I remember correctly, that was put there to handle some issues with finite precision and touching collisions (in dyn4j I don't consider touching a collision). If two shapes are touching, the origin will lie on an edge of the Minkowski Difference. When this happens, p1 or p2 could be the zero vector, which could cause some serious problems if the algorithm continued.
William
Hi William, In one of your comments, you said GJK was "Harder to get numerically stable" than SAT. what does that mean? Also, for the termination simplex, is that the same simplex we get from the GJK code when testing for intersection between two shapes?
@Andrew
What I'm trying to convey there is that there are cases where the GJK code can fail erroneously even in normal situations. They can all be fixed, but they aren't obvious right away. For example, lets look at the GJK collision post, containsOrigin method's line segment case (almost the very end of the post). Here we see that we use the Triple Product to obtain the normal vector of the line segment in the direction of the origin. This will yield a zero vector for the new search direction if the origin lies on the line segment. This can cause the algorithm to exit early. There are situations like this in the Closest Points and EPA code as well.
In this post I'm assuming that the Closest Points algorithm would create its own simplex. I suppose you could use the simplex from a failed GJK collision detection test, but you'll need to complete it if the GJK collision detection test failed before it has the requisite point count (not a big deal, just a thought). I need to add some more code here to explain a little further, since, for example, it's not really clear what the FindClosestEdge method does. I'll try to get something added to clear things up.
William
What does the findClosestEdge function do ? Does it return the closest point to the origin or does it return the closest edge that is made up of two points ?
@Andrew
I see what happened here. I recently combined this blog with another and the code was from a different post. I restored from a backup and now the code and intent should be clearer.
William
@Alex
Sorry about the confusion, I've updated the post to reflect the correct code sample. This was an issue when I moved the post to this blog. I suspect this was the source of Andrew's questions as well.
William
Thank you for the reply. Yes, I noticed that the earlier code sample was strangely similar to code in your EPA post.
Hello again!
Im having trouble with working out where the program actually exits and calls a collision.
I understand this is a collision as the objects are touching .
if (p.isZero()) {
return false;
}
Is this also a collision ? If so why is it returning true instead of false ?
if (dc – da < tolerance) {
distance = dc;
return true;
}
At the moment when my two objects collide i get stuck in an infinite loop where p doesn't equal vec2(0,0), and dc – da is no where near less then the tolerance. Also dc – da returns alot of negative values im not sure if that is meant to happen or not ? I am using 2 concave shapes for my collision test made out of straight lines, im not sure if this is a problem ?
Thanks!
@Alex
Correct, the first code block is to check for touching collision.
No, the second code block is to determine when we have found the closest edge on the Minkowski Difference (when we can terminate). So this should always return true when the shapes are separated.
The algorithm, as presented here, does not include a check for collision. Specifically, the post says:
One more problem that this algorithm can run into is if the shapes are actually intersecting. If they are intersecting the algorithm will never terminiate. This isn’t as big of a problem since most of the time you will determine if the shapes are colliding first anyway. If not, then we must add a check in the while loop for the simplex containing the origin. This can be done by a simple point in triangle test (2D).
William
Isn't it incorrect to simply check which point is further away from the origin and replace it with the new point?
It is pretty easy to compe up with a case where A is further away than B, yet the closest point on the resulting triangle actually lies on the segment AC, whereas your algorithm will result with the line BC.
@Riv
Correct. That should instead be:
p1 = findClosestPoint(origin, a, c);
p2 = findClosestPoint(origin, c, b);
// basically, which segment is closer
if (p1.magnitude() < p2.magnitude()) {
b = c;
} else {
a = c;
}
I've fixed it in the post.
William
How did you get a direction = (1, -3) in the beginning of second iteration?
The closest point to origin from line segment (-11, -1) to (1, 3) is (-1.8, 2.4) so shouldn't this be the new direction?
And to get a point on Minkowski difference that is closer to the origin shouldn't this be negated?
The pseudo-code doesn't seem to do so, just takes the closest point on line segment as direction itself.
@Monty
You are correct. I made a mistake in my calculation the last time I updated the post. That should be (-0.8, 2.4):
a = (1, 3)
b = (-11, -1)
AB = (-11 - 1, -1 - 3) = (-12, -4) = (-3, -1)
AO = (0 - 1, 0 - 3) = (-1, -3)
AO.dot(AB) = -1 * -3 + -3 * -1 = 3 + 3 = 6
AB.dot(AB) = -3 * -3 + -1 * -1 = 9 + 1 = 10
t = 3/5
AB.mult(t).add(A) = (-9/5 + 5/5, -3/5 + 15/5) = (-4/5, 12/5) = (-0.8, 2.4)
This was due to my last update to the post again. The d.negate() should be inside the while loop.
Thanks for pointing these out. I have fixed both within the post.
William
Iteration 2 isn't making sense to me.
dc and da should not be equal to -3 and -8 respectively, correct?
My understanding here is that is:
d = (0.8, -2.4)
First point on the simplex at this stage is (1, 3)
Support C is calculated successfully as (-4, -1)
dc = (0.8, -2.4).dotProd(-4, -1) = -3.2 + 2.4 = -0.8
da = (0.8, -2.4).dotProd(1, 3) = 0.8 – 7.2 = -6.4
This numerical difference is throwing off my distance calculation between the two objects.
Can you please explain how you determined the values of dc and da in this iteration?
@Jordan
The values were wrong. I've updated the post accordingly. After editing so much, I must have missed this section.
Thanks,
William
Thanks William,
This lines up perfectly with the implementation I have now.
Only problem (I assume you may have forgotten to change this when updating there) is that the final value you have calculated for distance should probably also correspond to 2.95 (the value of dc in this iteration), and not the old value of 1.72. But that said, this doesn't seem to line up with diagram 1 then!
@Jordan
The value of 1.72 is still correct (well mostly, the rounding was off).
The problem was that c.dot(d) isn't the distance because d isn't normalized. We can improve performance by avoiding the normalization until we've found the closest edge to the origin.
I've added some comments and fixed the code to reflect this. I've also updated the Distance section to reflect the correct values (by using the same precision).
William
Thanks a lot for the clarification, William. That was a great help.
I ended up solving the issue in my own way but this would suit better.
The tutorial was a great help!
This is a very helpful tutorial, however I'm having problems with the 3D algorithm. I implemented it exactly as you did, and it works, however not all the time. I've found that it doesn't always calculate the correct point, as I can move one of my objects on an axis perpendicular to the closest face on the other, and the calculated closest point will move, which it obviously shouldn't be doing. Upon closer inspection, I found that the direction that I initiate with actually causes this point to be in different locations, and occasionally crashes my program. Is there an initial direction that I should use? I've already used the center of one set of points minus the center of the other set.
I mostly fixed it. I was just doing something dumb that was hard to notice. However there is still the problem of the occasional crash. Normally this happens when you try to test a single point against an axis aligned box. The algorithm gets stuck in a loop because the 4th point of the simplex it calculates later turns out to be the furthest point away, so that point gets removed from the simplex, and then re-added because it calculates the same point again. Do you have any advice to remedy this?
I'm glad to hear you worked out your other problem.
There are some corner cases to work out for sure. Have you looked at my 2D implementation? I specifically try to handle the "new point is on the simplex" case. This is probably not sufficient for 3D, but worth a look at if you haven't already. You'll also notice that my loop gives up after a certain number of iterations as well.
I haven't thought through all the corner cases that could be possible in 3D, but I've found that the best way to troubleshoot issues like these are to have a test application that can log the position/rotation of the objects after every move. Then, when the corner case hits (the app crashing or hanging actually helps here), you can use the last printed data to setup a specific test that you can step through with a debugger (and pen+paper).
William
I'm not entirely sure what you did to handle these cases in 2D just by looking at your code. Do you mind explaining what you did so I can better understand?
Sorry, I may not have been clear. I was simply showing that corner cases are possible and that my post certainly didn't attempt to cover them. The link to my 2D implementation was really just to have another source to compare against, not to point to a specific solution.
Thinking out loud... So you have a triangular simplex. The next point you get should be along the normal of the triangular simplex in the direction of the origin. This shouldn't give you a point in the opposite direction of the origin. Are you using the triple product to calculate the simplex normal? This can cause problems in some cases like when the simplex is degenerate (all points are the same or two points are the same). It can also cause problems if the origin lies on the simplex's face as well.
I'm not sure what else to suggest without being able to examine the code and the configuration of the shapes when the problem occurs.
William
what are the algorithms to determine distance between convex hulls in non-intersecting case? I read that GJK slows down once its near convergence. I am looking for faster ones.
@shome
It's been a while since I've looked into it. The only ones I remember coming across are Lin-Canny Closest Features Algorithm and another that was based off of it. There was some question of one of those being patented so I didn't look too deep into those.
In my experience, GJK will only slow down near convergence for rounded or ill-conditioned shapes. If your shapes are all polytopes, then it should be lightning fast.
William
I think you made a mistake in the section "The distance". If the t parameter is greater than 1 or smaller that 0, which can happen with the dot product, you'll end up with a point that doesnt lie on the segment. The solution to that problem would be to clamp t to [0;1], in order to only get a point on the segment.
Although your tuturial was very helpful and easy to follow, I found some issues:
– On the first iteration, you picked ‘p’ as (1, 3), when the
calculation yelds (1.7, 2.51).
– In the situation shown on fig1.jpg the minkowski difference (blue dots)
doesn’t contain the origin(white dot), but still, the closestPointToOrigin()
routine returns (0,0);
To fix that, before the return i put the following statements:
if the found point is between a and b
return it
else if a.magnitude() < b.magnitude()
return a
else
return b
And the result is fig2.jpg, note that p is the same as a.
F.Y.I: the squares are 20×20 pixels.
Could you give me a opinion about that?
Thank you!
–
fig1.jpg : http://img210.imageshack.us/i/fig1k.jpg/
fig2.jpg : http://img195.imageshack.us/i/fig2ih.jpg/